The formatter threw an exception while trying to deserialize the message: Error in deserializing body of request message for operation 'Translate'. The maximum string content length quota (30720) has been exceeded while reading XML data. This quota may be increased by changing the MaxStringContentLength property on the XmlDictionaryReaderQuotas object used when creating the XML reader. Line 2, position 33807.
The formatter threw an exception while trying to deserialize the message: Error in deserializing body of request message for operation 'Translate'. The maximum string content length quota (30720) has been exceeded while reading XML data. This quota may be increased by changing the MaxStringContentLength property on the XmlDictionaryReaderQuotas object used when creating the XML reader. Line 1, position 34276.
We recall Brouwer’s famous fixed point theorem:
Theorem 1 (Brouwer fixed point theorem) Let 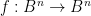 be a continuous function on the unit ball
be a continuous function on the unit ball 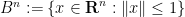 in a Euclidean space
in a Euclidean space 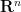 . Then
. Then 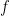 has at least one fixed point, thus there exists
has at least one fixed point, thus there exists  with
with  .
.
This theorem has many proofs, most of which revolve (either explicitly or implicitly) around the notion of the degree of a continuous map 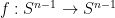 of the unit sphere
of the unit sphere  to itself, and more precisely around the stability of degree with respect to homotopy. (Indeed, one can view the Brouwer fixed point theorem as an assertion that some non-trivial degree-like invariant must exist, or more abstractly that the homotopy group
to itself, and more precisely around the stability of degree with respect to homotopy. (Indeed, one can view the Brouwer fixed point theorem as an assertion that some non-trivial degree-like invariant must exist, or more abstractly that the homotopy group 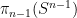 is non-trivial.)
is non-trivial.)
One of the many applications of this result is to prove Brouwer’s invariance of domain theorem:
Theorem 2 (Brouwer invariance of domain theorem) Let  be an open subset of
be an open subset of 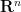 , and let
, and let 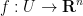 be a continuous injective map. Then
be a continuous injective map. Then  is also open.
is also open.
This theorem in turn has an important corollary:
Corollary 3 (Topological invariance of dimension) If  , and
, and  is a non-empty open subset of
is a non-empty open subset of 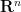 , then there is no continuous injective mapping from
, then there is no continuous injective mapping from  to
to 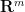 . In particular,
. In particular, 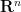 and
and 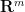 are not homeomorphic.
are not homeomorphic.
This corollary is intuitively obvious, but note that topological intuition is not always rigorous. For instance, it is intuitively plausible that there should be no continuous surjection from 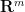 to
to 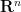 for
for  , but such surjections always exist, thanks to variants of the Peano curve construction.
, but such surjections always exist, thanks to variants of the Peano curve construction.
Theorem 2 or Corollary 3 can be proven by simple ad hoc means for small values of 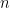 or
or 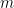 (for instance, by noting that removing a point from
(for instance, by noting that removing a point from 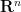 will disconnect
will disconnect 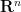 when
when 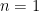 , but not for
, but not for 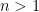 ), but I do not know of any proof of these results in general dimension that does not require algebraic topology machinery that is at least as sophisticated as the Brouwer fixed point theorem. (Lebesgue, for instance, famously failed to establish the above corollary rigorously, although he did end up discovering the important concept of Lebesgue covering dimension as a result of his efforts.)
), but I do not know of any proof of these results in general dimension that does not require algebraic topology machinery that is at least as sophisticated as the Brouwer fixed point theorem. (Lebesgue, for instance, famously failed to establish the above corollary rigorously, although he did end up discovering the important concept of Lebesgue covering dimension as a result of his efforts.)
Nowadays, the invariance of domain theorem is usually proven using the machinery of singular homology. In this post I would like to record a short proof of Theorem 2 using Theorem 1 that I discovered in a paper of Kulpa, which avoids any use of algebraic topology tools beyond the fixed point theorem, though it is more ad hoc in its approach than the systematic singular homology approach.
Remark 1 A heuristic explanation as to why the Brouwer fixed point theorem is more or less a necessary ingredient in the proof of the invariance of domain theorem is that a counterexample to the former result could conceivably be used to create a counterexample to the latter one. Indeed, if the Brouwer fixed point theorem failed, then (as is well known) one would be able to find a continuous function  that was the identity on
that was the identity on 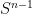 (indeed, one could take
(indeed, one could take 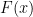 to be the first point in which the ray from
to be the first point in which the ray from 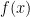 through
through  hits
hits 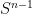 ). If one then considered the function
). If one then considered the function 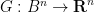 defined by
defined by  , then this would be a continuous function which avoids the interior of
, then this would be a continuous function which avoids the interior of 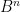 , but which maps the origin
, but which maps the origin 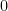 to a point on the sphere
to a point on the sphere 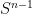 (and maps
(and maps 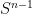 to the dilate
to the dilate 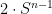 ). This could conceivably be a counterexample to Theorem 2, except that
). This could conceivably be a counterexample to Theorem 2, except that  is not necessarily injective. I do not know if there is a more rigorous way to formulate this connection.
is not necessarily injective. I do not know if there is a more rigorous way to formulate this connection.
The reason I was looking for a proof of the invariance of domain theorem was that it comes up in the very last stage of the solution to Hilbert’s fifth problem, namely to establish the following fact:
Theorem 4 (Hilbert’s fifth problem) Every locally Euclidean group is isomorphic to a Lie group.
Recall that a locally Euclidean group is a topological group which is locally homeomorphic to an open subset of a Euclidean space 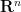 , i.e. it is a continuous manifold. Note in contrast that a Lie group is a topological group which is locally diffeomorphic to an open subset of
, i.e. it is a continuous manifold. Note in contrast that a Lie group is a topological group which is locally diffeomorphic to an open subset of 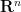 , it is a smooth manifold. Thus, Hilbert’s fifth problem is a manifestation of the “rigidity” of algebraic structure (in this case, group structure), which turns weak regularity (continuity) into strong regularity (smoothness).
, it is a smooth manifold. Thus, Hilbert’s fifth problem is a manifestation of the “rigidity” of algebraic structure (in this case, group structure), which turns weak regularity (continuity) into strong regularity (smoothness).
It is plausible that something like Corollary 3 would need to be invoked in order to solve Hilbert’s fifth problem. After all, if Euclidean spaces 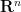 ,
, 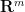 of different dimension were homeomorphic to each other, then the property of being locally Euclidean loses a lot of meaning, and would thus not be a particularly powerful hypothesis. Note also that it is clear that two Lie groups can only be isomorphic if they have the same dimension, so in view of Theorem 4, it becomes plausible that two Euclidean spaces can only be homeomorphic if they have the same dimension, although I do not know of a way to rigorously deduce this claim from Theorem 4.
of different dimension were homeomorphic to each other, then the property of being locally Euclidean loses a lot of meaning, and would thus not be a particularly powerful hypothesis. Note also that it is clear that two Lie groups can only be isomorphic if they have the same dimension, so in view of Theorem 4, it becomes plausible that two Euclidean spaces can only be homeomorphic if they have the same dimension, although I do not know of a way to rigorously deduce this claim from Theorem 4.
Interestingly, Corollary 3 is the only place where algebraic topology enters into the solution of Hilbert’s fifth problem (although its cousin, point-set topology, is used all over the place). There are results closely related to Theorem 4, such as the Gleason-Yamabe theorem mentioned in a recent post, which do not use the notion of being locally Euclidean, and do not require algebraic topological methods in their proof. Indeed, one can deduce Theorem 4 from the Gleason-Yamabe theorem and invariance of domain; we sketch a proof of this (following Montgomery and Zippin) below the fold.
— 1. Invariance of domain — Now we prove Theorem 2. By rescaling and translation invariance, it will suffice to show the following claim:
Theorem 5 (Invariance of domain, again) Let 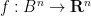 be an continuous injective map. Then
be an continuous injective map. Then 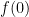 lies in the interior of
lies in the interior of  .
.
Let 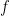 be as in Theorem 5. The map
be as in Theorem 5. The map 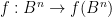 is a continuous bijection between compact Hausdorff spaces and is thus a homeomorphism. In particular, the inverse map
is a continuous bijection between compact Hausdorff spaces and is thus a homeomorphism. In particular, the inverse map  is continuous. Using the Tietze extension theorem, we can find a continuous function
is continuous. Using the Tietze extension theorem, we can find a continuous function  that extends
that extends  .
.
The function  has a zero on
has a zero on  , namely at
, namely at 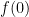 . We can use the Brouwer fixed point theorem to show that this zero is stable:
. We can use the Brouwer fixed point theorem to show that this zero is stable:
Lemma 6 (Stability of zero) Let 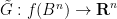 be a continuous function such that
be a continuous function such that  for all
for all  . Then
. Then  has at least one zero (i.e. there is an
has at least one zero (i.e. there is an 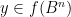 such that
such that 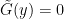 ).
).
Proof: Apply Theorem 1 to the function
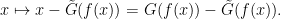

Now suppose that Theorem 5 failed, so that 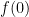 is a not an interior point of
is a not an interior point of  . We will use this to locate a small perturbation of
. We will use this to locate a small perturbation of  that no longer has a zero on
that no longer has a zero on  , contradicting Lemma 6.
, contradicting Lemma 6.
We turn to the details. Let 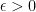 be a small number to be chosen later. By continuity of
be a small number to be chosen later. By continuity of  , we see (if
, we see (if  is small enough) that we have
is small enough) that we have  whenever
whenever 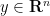 and
and 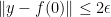 .
.
On the other hand, since 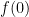 is not an interior point of
is not an interior point of  , there exists a point
, there exists a point 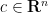 with
with 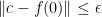 that lies outside
that lies outside  . By translating
. By translating 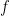 if necessary, we may take
if necessary, we may take 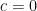 ; thus
; thus  avoids zero,
avoids zero, 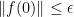 , and we have
, and we have 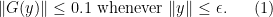
Let  denote the set
denote the set 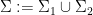 , where
, where

and 
By construction,  is compact but does not contain
is compact but does not contain 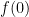 . It is a perturbation of
. It is a perturbation of  , and crucially there is a continuous map
, and crucially there is a continuous map 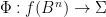 defined by setting
defined by setting 
Note that 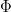 is continuous and well-defined since
is continuous and well-defined since  avoids zero.
avoids zero.
By construction,  is non-zero on
is non-zero on 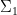 ; since
; since 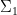 is compact,
is compact,  is bounded from below on
is bounded from below on 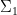 by some
by some ![{0 . </P><P>By the Weierstrass approximation theorem, we can find a polynomial <IMG class=latex title=]() such that
such that ![\displaystyle \| P(y) - G(y) \| </P><P>for all <IMG class=latex title=]() ; in particular,
; in particular, 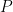 does not vanish on
does not vanish on 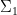 . At present, it is possible that
. At present, it is possible that 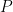 vanishes on
vanishes on 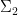 . But as
. But as 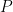 is smooth and
is smooth and 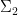 has measure zero,
has measure zero, 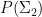 also has measure zero; so by shifting
also has measure zero; so by shifting 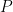 by a small generic constant we may assume without loss of generality that
by a small generic constant we may assume without loss of generality that 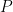 also does not vanish on
also does not vanish on 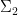 . (If one wishes, one can use an algebraic geometry argument here instead of a measure-theoretic one, noting that
. (If one wishes, one can use an algebraic geometry argument here instead of a measure-theoretic one, noting that 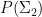 lies in an algebraic hypersurface and can thus be generically avoided by perturbation. A purely topological way to avoid zeroes in
lies in an algebraic hypersurface and can thus be generically avoided by perturbation. A purely topological way to avoid zeroes in 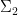 is also given in Kulpa’s paper.)
is also given in Kulpa’s paper.)
Now consider the function 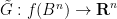 defined by
defined by
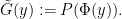
This is a continuous function that is never zero. From (3), (2) we have ![\displaystyle \| G(y) - \tilde G(y) \| </P><P>whenever <IMG class=latex title=]() is such that
is such that 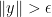 . On the other hand, if
. On the other hand, if 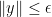 , then from (2), (1) we have
, then from (2), (1) we have 
and hence by (3) and the triangle inequality 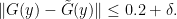
Thus in all cases we have
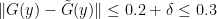
for all 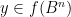 . But this, combined with the non-vanishing nature of
. But this, combined with the non-vanishing nature of  , contradicts Lemma 6.
, contradicts Lemma 6.
— 2. Hilbert’s fifth problem — We now sketch how invariance of domain can be used to establish the solution to Hilbert’s fifth problem (as formulated in Theorem 4). Our main tool is the Gleason-Yamabe theorem, in the form stated in Theorem 4 of this previous post:
Theorem 7 (Gleason-Yamabe theorem) Every locally compact Hausdorff group has an open subgroup that is the projective limit of Lie groups.
A locally Euclidean group is of course locally compact Hausdorff; it is also first countable, and hence (by the Birkhoff-Kakutani theorem, discussed in this post) is also metrisable. Because of this, it is not difficult to show that the open subgroup given by the Gleason-Yamabe theorem in this case can be obtained as a projective limit

of a countable sequence 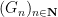 of Lie groups, with continuous homomorphisms from
of Lie groups, with continuous homomorphisms from 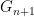 to
to 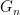 for each
for each 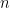 .
.
Using Cartan’s theorem to obtain the smoothness of outer automorphisms on Lie groups as in previous posts, we see that to show that a topological group is a Lie group, it suffices to locate an open subgroup that is a Lie group. In view of these reductions, it suffices to show
Proposition 8 Let  be a locally Euclidean group that is the inverse limit
be a locally Euclidean group that is the inverse limit 
of Lie groups. Then  is itself isomorphic to a Lie group.
is itself isomorphic to a Lie group.
We now prove the proposition. We first observe by shrinking the 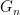 if necessary (and using Cartan’s theorem that locally compact subgroups of a Lie group are still Lie) we may assume that all the projection maps in the inverse limit are surjective; indeed, by local compactness we may take
if necessary (and using Cartan’s theorem that locally compact subgroups of a Lie group are still Lie) we may assume that all the projection maps in the inverse limit are surjective; indeed, by local compactness we may take 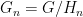 where
where 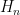 are a sequence of compact normal subgroups converging to the identity.
are a sequence of compact normal subgroups converging to the identity.
As continuous homomorphisms of Lie groups are automatically smooth (as proven in this previous post), the projection maps from 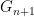 to
to 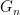 induce an associated projection map from
induce an associated projection map from 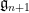 to
to 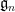 at the Lie algebra level. As the former maps are surjective, the latter maps are also. In particular, the dimensions of the finite-dimensional Lie algebras
at the Lie algebra level. As the former maps are surjective, the latter maps are also. In particular, the dimensions of the finite-dimensional Lie algebras 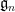 are non-decreasing in
are non-decreasing in 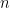 .
.
Another consequence of surjectivity is that every tangent vector in 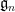 can be lifted up to
can be lifted up to 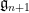 . Continuing this process and passing to the inverse limit, it is possible to show that every one-parameter subgroup in one of the factor groups
. Continuing this process and passing to the inverse limit, it is possible to show that every one-parameter subgroup in one of the factor groups 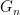 can be lifted up (locally, at least) to a one-parameter subgroup of
can be lifted up (locally, at least) to a one-parameter subgroup of  . In fact, one can show that a neighbourhood of the origin in
. In fact, one can show that a neighbourhood of the origin in 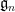 can be lifted up into
can be lifted up into  , to provide a continuous injection of an open subset of that Lie algebra into
, to provide a continuous injection of an open subset of that Lie algebra into  .
.
Now we crucially use the invariance of domain (Corollary 3) to conclude that the dimensions of the Lie algebras 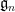 must be bounded in
must be bounded in 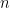 (indeed, they cannot exceed the dimension of the locally Euclidean group
(indeed, they cannot exceed the dimension of the locally Euclidean group  ). As these dimensions are non-decreasing, they must therefore be eventually constant; by discarding finitely many of the factor groups, we may thus assume that all the
). As these dimensions are non-decreasing, they must therefore be eventually constant; by discarding finitely many of the factor groups, we may thus assume that all the 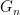 have the same dimension. In particular, the kernels of the projection maps from
have the same dimension. In particular, the kernels of the projection maps from 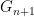 to
to 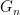 are zero-dimensional Lie groups and are thus discrete. As
are zero-dimensional Lie groups and are thus discrete. As 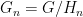 , this means that the
, this means that the 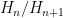 are also discrete, thus
are also discrete, thus 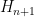 is an open subgroup of
is an open subgroup of 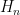 , and so (by compactness of
, and so (by compactness of 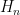 ) has finite index. As the
) has finite index. As the 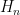 converge to the trivial group as
converge to the trivial group as 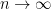 , we conclude that each of the
, we conclude that each of the 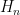 are profinite, and in particular are totally disconnected. Thus, for any
are profinite, and in particular are totally disconnected. Thus, for any 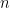 , we have a short exact sequence
, we have a short exact sequence

describing  as the extension of a Lie group
as the extension of a Lie group 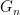 by a totally disconnected compact group
by a totally disconnected compact group 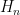 . Furthermore, we can lift a small neighbourhood of the identity of
. Furthermore, we can lift a small neighbourhood of the identity of 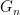 to
to  in a continuously injective manner. This neighbourhood is connected, and acts on the normal subgroup
in a continuously injective manner. This neighbourhood is connected, and acts on the normal subgroup 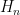 by conjugation. But
by conjugation. But 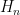 is totally disconnected, and so all orbits of this action must be points; thus, the lift of this neighbourhood commutes with
is totally disconnected, and so all orbits of this action must be points; thus, the lift of this neighbourhood commutes with 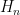 . As a consequence, one can show that
. As a consequence, one can show that  has the local topological (and group) structure of the direct product
has the local topological (and group) structure of the direct product 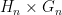 . But
. But  is also locally Euclidean; as
is also locally Euclidean; as 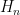 is totally disconnected, these two statements are only compatible if
is totally disconnected, these two statements are only compatible if 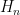 is discrete. Thus the Lie group
is discrete. Thus the Lie group 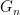 is an open subgroup of
is an open subgroup of  , and we are done.
, and we are done.
Remark 2 The above argument shows that any metrisable group which is “finite-dimensional” in the sense that it does not contain continuous injective images of non-trivial open sets of Euclidean spaces 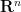 of arbitrarily large dimension, has the local structure (as a topological space) of the product of a Euclidean space and a totally disconnected space. Of course, direct products of Lie groups and totally disconnected groups provide one such example of this claim. A more non-trivial example is given by the solenoid groups, a simple example of which is the (additive) group
of arbitrarily large dimension, has the local structure (as a topological space) of the product of a Euclidean space and a totally disconnected space. Of course, direct products of Lie groups and totally disconnected groups provide one such example of this claim. A more non-trivial example is given by the solenoid groups, a simple example of which is the (additive) group 
where  is the diagonally embedded copy of the integers. This is a compact Hausdorff group that has a short exact sequence
is the diagonally embedded copy of the integers. This is a compact Hausdorff group that has a short exact sequence 
and has the local structure of 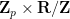 , although
, although 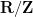 does not embed into this group and so this is not a direct or semi-direct product. (Topologically, it can be viewed as the set
does not embed into this group and so this is not a direct or semi-direct product. (Topologically, it can be viewed as the set ![{{\bf Z}_p \times [0,1]} {{\bf Z}_p \times [0,1]}](http://s0.wp.com/latex.php?latex=%7B%7B%5Cbf+Z%7D_p+%5Ctimes+%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0) after identifying
after identifying 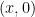 with
with 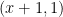 for every
for every  -adic integer
-adic integer  .) It has topological dimension one, in the sense that it contains continuous injective images of open subsets of
.) It has topological dimension one, in the sense that it contains continuous injective images of open subsets of 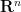 if and only if
if and only if  . It is also the projective limit of the Lie groups
. It is also the projective limit of the Lie groups 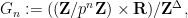
each of which is isomorphic to the circle 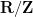 , but in a manner which becomes increasingly “twisted” as
, but in a manner which becomes increasingly “twisted” as 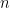 increases (which helps explain the terminology “solenoid”). It is an instructive exercise to verify that
increases (which helps explain the terminology “solenoid”). It is an instructive exercise to verify that  is connected, but not path connected or locally connected. Thus we see that connected locally compact groups can contain some significant non-Lie behaviour, even in the abelian setting.
is connected, but not path connected or locally connected. Thus we see that connected locally compact groups can contain some significant non-Lie behaviour, even in the abelian setting.
Remark 3 Of course, it is possible for locally compact groups to be infinite-dimensional; a simple example is the infinite-dimensional torus 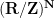 , which is compact, abelian, metrisable, and locally connected, but infinite dimensional. (It will still be an inverse limit of Lie groups, though.)
, which is compact, abelian, metrisable, and locally connected, but infinite dimensional. (It will still be an inverse limit of Lie groups, though.)
Remark 4 The above analysis also gives another purely topological characterisation of Lie groups; a topological group is Lie if and only if it is locally compact, Hausdorff, first-countable, locally connected, and finite-dimensional. It is interesting to note that this characterisation barely uses the real numbers 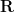 , which are of course fundamental in defining the smooth structure of a Lie group; the only remaining reference to
, which are of course fundamental in defining the smooth structure of a Lie group; the only remaining reference to 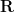 comes through the notion of finite dimensionality. It is also possible, using dimension theory, to obtain alternate characterisations of finite dimensionality (e.g. finite Lebesgue covering dimension) that avoid explicit mention of the real line, thus capturing the concept of a Lie group using only the concepts of point-set topology (and the concept of a group, of course).
comes through the notion of finite dimensionality. It is also possible, using dimension theory, to obtain alternate characterisations of finite dimensionality (e.g. finite Lebesgue covering dimension) that avoid explicit mention of the real line, thus capturing the concept of a Lie group using only the concepts of point-set topology (and the concept of a group, of course).
 How can we rethink the current Math education paradigm to consider the wealth of available technology? Can video games teach basic math skills or are they just a waste of time? Video game helps students to Math proficiency? What are the key elements in a game that promotes the mastery of mathematics? These are some of the "game change" questions, Keith Devlin tackles in his new book "mathematics education of a new era: video games as a Medium
How can we rethink the current Math education paradigm to consider the wealth of available technology? Can video games teach basic math skills or are they just a waste of time? Video game helps students to Math proficiency? What are the key elements in a game that promotes the mastery of mathematics? These are some of the "game change" questions, Keith Devlin tackles in his new book "mathematics education of a new era: video games as a Mediumfor learning."

 "Stan Wagon, and have exchanged a
"Stan Wagon, and have exchanged a 